Voici réunis en une seule circonférence, les principaux polygones représentés par leur côté.

Tracez un cercle et ses deux diamètres perpendiculaires.

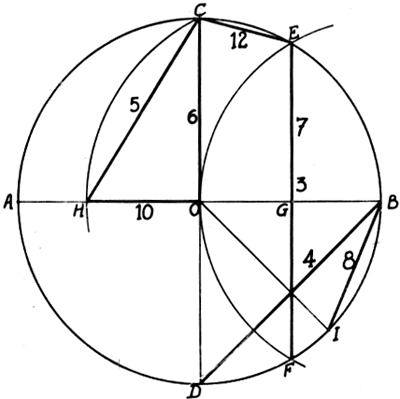
Le triangle équilatéral (3)

En gardant le même rayon faites un arc de cercle de centre B de telle façon qu'il coupé le premier cercle en E et F, cette droite est un côté du triangle EFA.

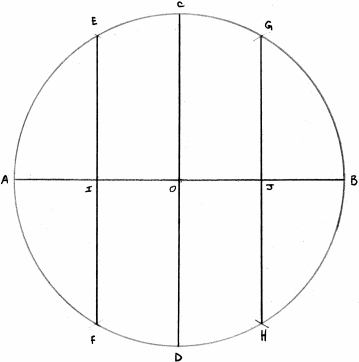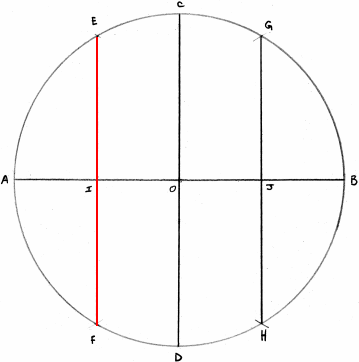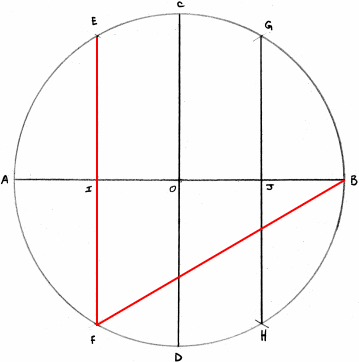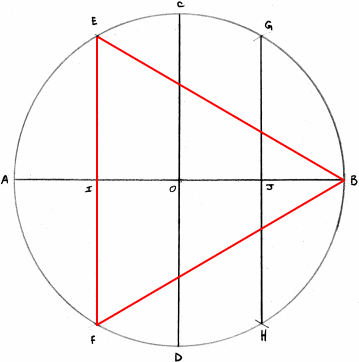
Le carré (4)

BD est un côté du carré BDAC.

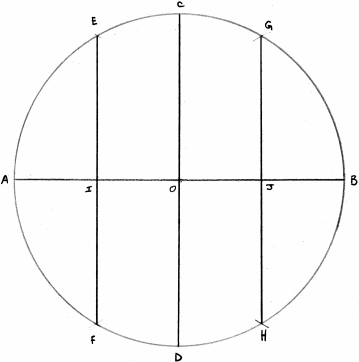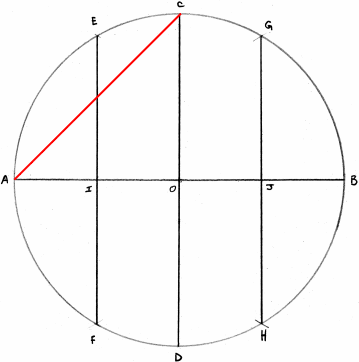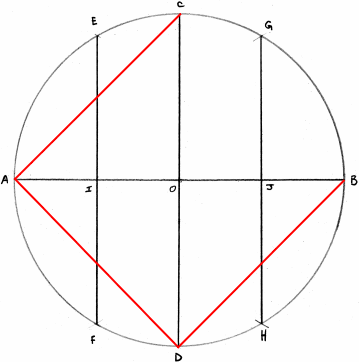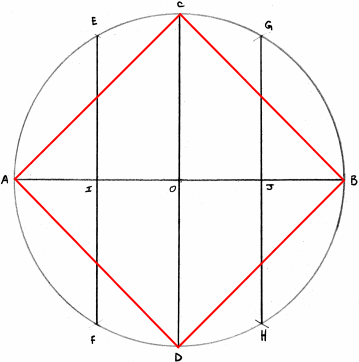
Le pentagone (5)

Prenez le milieu de OB soit G; mettez la pointe sèche du compas en G et tracez un arc de cercle passant par C et coupant OA en H; la corde de cet arc, soit CH, est un côté du pentagone.

Mettez la pointe sèche du compas en C puis reportez le côté CH cinq fois sur le cercle.

L'hexagone (6)

Son côté est égal au rayon du cercle.

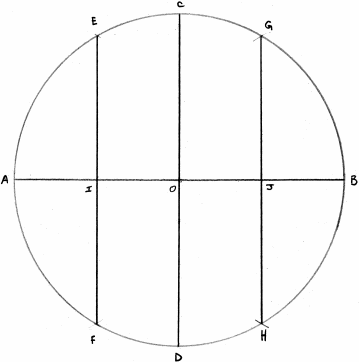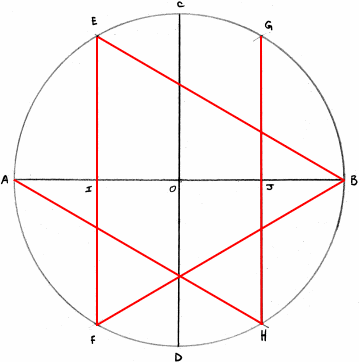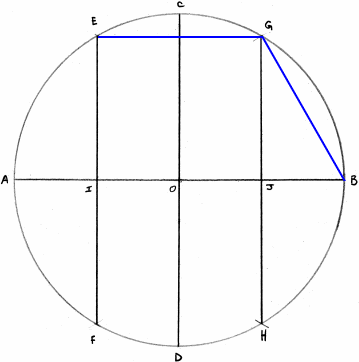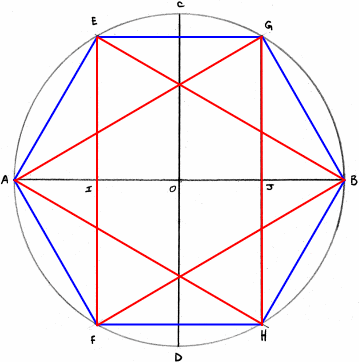
L'octogone (8)

Tracez un rayon passant par l'intersection de EF, côté du triangle équilatéral, et de BD, côté du carré, vous obtenez le point I sur la circonférence ; BI est un côté de l'octogone.

Le décagone (10)

Refaites la construction du pentagone, le côté cherché est égal à la distance entre le point H sur le diamètre horizontal et le centre O.

Le dodécagone (12)

Reprenez la construction du triangle équilatéral, le côté est la droite tracée entre C et E.